Windows Move Command | Move Files From One Folder to Another in CMD
In the Windows Command Prompt, we use the move command to move files from one directory to another (cut and paste).
The syntax of the move command is as follows:
move <Source> <Target>We can also use the move command to move folders from one location to another.
Command Options
| /Y | Do not ask for confirmation if a duplicate file is found at the destination. The destination file will be overwritten. |
| /-Y | Ask before overwriting destination files. |
Examples
Move sales.doc in the current directory to C:\backup directory:
move sales.doc C:\backupMove C:\data\sales.doc to C:\backup directory. The file will be overwritten if it already exists in the destination folder:
move /y C:\data\sales.doc C:\backupMove C:\data\finance to C:\backup folder:
move C:\data\finance C:\backupMove all files in a directory
You can use wildcards with the move command. For example, the following command moves all files in the C:\data to C:\backup.
move /y C:\data\* C:\backupThe following command moves all files with a .doc extension to the backup folder:
move /y C:\data\*.doc C:\backupIn the following example, all files whose names start with screenshot are moved to the C:\backup directory.
move /y C:\data\screenshot* C:\backup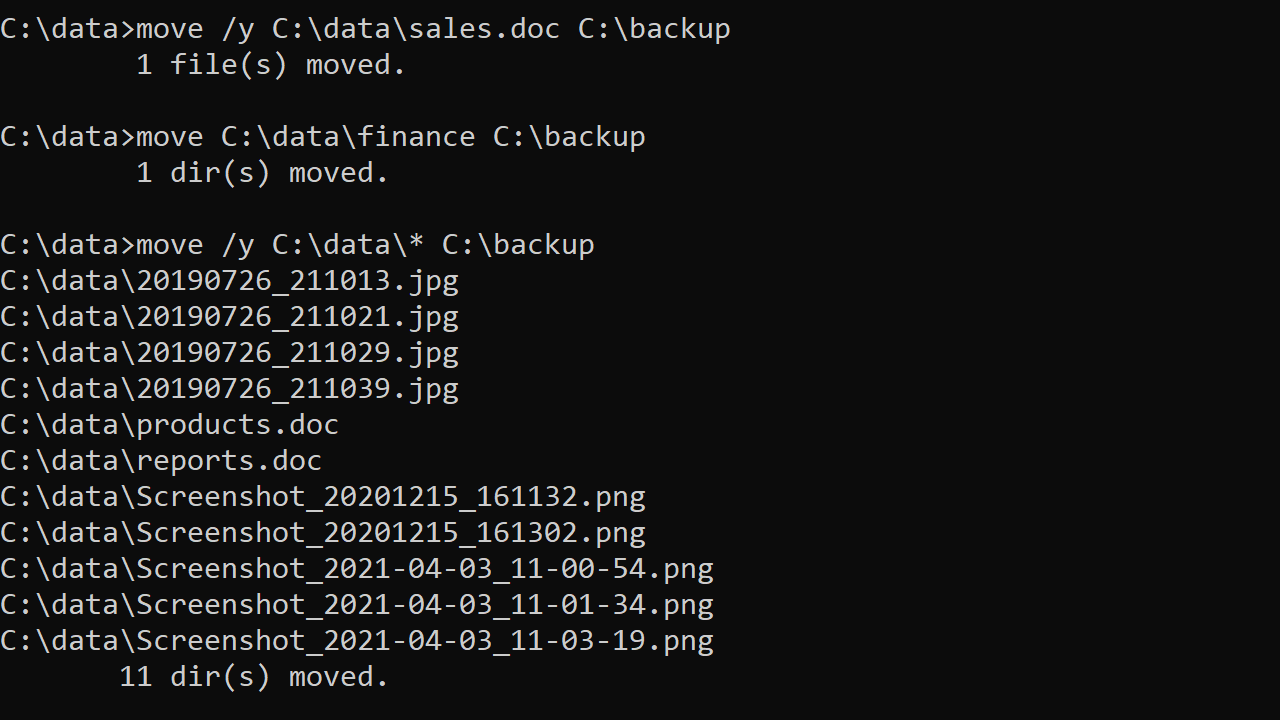
Move two or more files
To move two or more files without using wildcards, you have to use a for loop, as shown in the following example:
for %i in (sales.doc, products.doc) do move /y %i C:\backupIf you want to run the for command in a batch file, you would use two % (%%) with the variable.
for %%i in (sales.doc, products.doc) do move /y %%i C:\backupThe move command deletes the source file after it is copied to the destination. If you want to keep the original file, use the copy or xcopy.